Soft soil
Das Weiche-Boden-Modell, ursprünglich in [1] vorgeschlagen, soll seine Anwendung in der Modellierung von erheblich weichen Böden mit hohem Kompressionsgrad finden, für die die Anwendung des Härtebodenmodells möglicherweise unzureichend ist. Ähnlich wie das Härtebodenmodell wird das Weiche-Boden-Modell durch zwei Fließflächen dargestellt. Die Scherfließfläche basiert auf dem Matsuoka-Nakai-Versagens-Kriterium und die Kompressionskappe wird hier auf der Grundlage des Generalisierten Cam-Clay-Modells formuliert. Ihre Projektionen in die deviatorische Ebene sind glatte konvexe Kurven, die durch die Ecken des Mohr-Coulomb-Modells verlaufen. Eine grafische Darstellung ist in der folgenden Abbildung dargestellt.
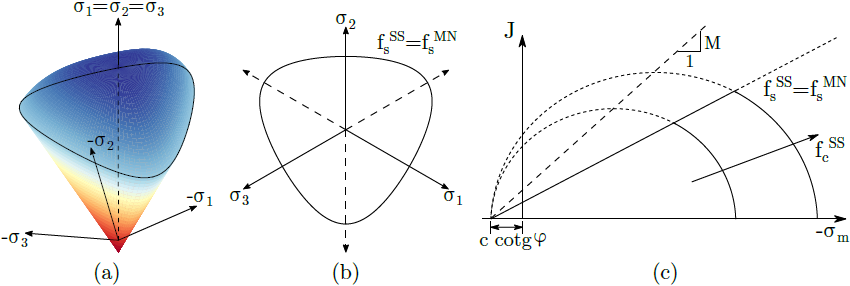a) Fließfläche im Hauptspannungsraum, b) Projektion in die deviatorische Ebene und c) Meridianebene
Im Gegensatz zum Generalisierten Cam-Clay-Modell wird die Steigung der kritischen Zustandslinie M in Abhängigkeit vom seitlichen Erddruckbeiwert K0N und den Steifigkeitsparametern κ*, λ* folgendermaßen definiert:
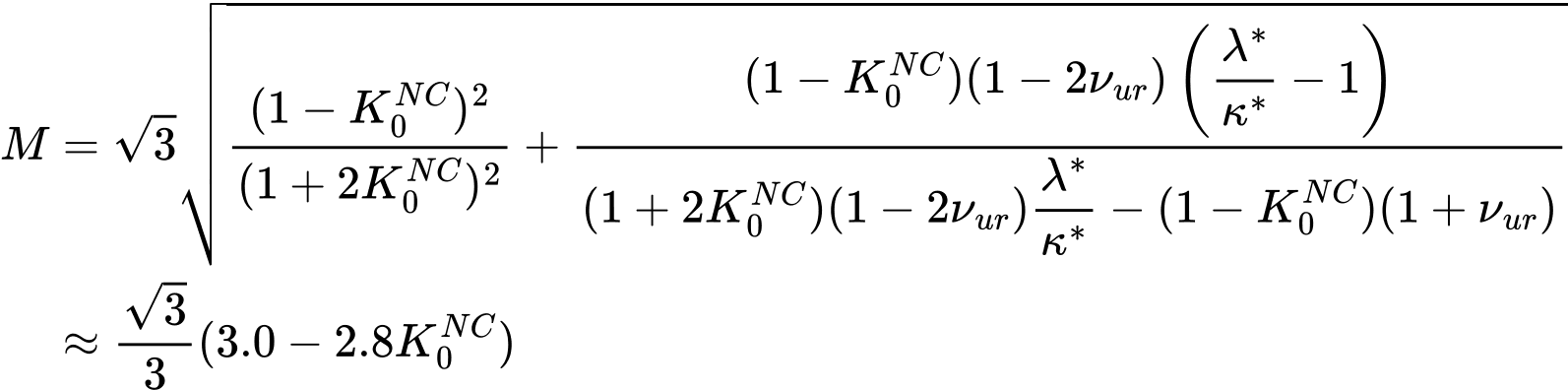
Weitere Details zu den Parametern κ*, λ* sind in der Beschreibung des Modifizierten Cam-Clay-Modells zu finden. Der Grund für diese besondere Definition ist, dass für Böden der Wert des Parameters M im Modifizierten Cam-Clay-Modell einen richtigen Scherwiderstand angibt, was darauf hinweist, dass der Wert von K0NC den durch die Jaky-Formel für einen gegebenen Wert des inneren Reibungswinkels φvorgeschlagenen Wert erheblich überschreiten könnte. Weitere Details sind in [1] zu finden.
Die Scherfließfläche wird so angenommen, dass sie dem Verhalten des elastisch-perfekt-plastischen Materialmodells entspricht. Auf der anderen Seite kann die Kompressionskappe, im Gegensatz zum Generalisierten Cam-Clay-Modell, nur weiter verhärten. Mit anderen Worten, der Vorkonsolidierungsdruck pc der die Entwicklung der Kompressionskappe steuert, kann nur steigen. Weitere Informationen hierzu finden Sie im Modifizierten Cam-Clay-Modell.Diese Einschränkung führt zu bestimmten Einschränkungen bei der Auswahl der Modellparameter, insbesondere beim Wert des inneren Reibungswinkels φ. Es muss die folgende Bedingung erfüllt sein:
Diese Bedingung muss auch erfüllt sein, wenn:
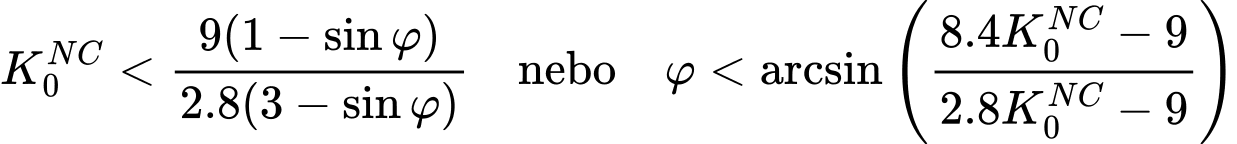
Eine graphische Beziehung zwischen der Scherfließfläche und der Kompressionskappe wird in der folgenden Abbildung für zwei verschiedene Werte von K0NC und mehrere Werte des inneren Reibungswinkels φ für feste Werte der Parameter κ*, λ*, ν dargestellt. Es wird klar, dass für die Kombination von M(K0NC = 0.6) = 0.774 und φ = 40° die oben genannten Bedingungen nicht für die erste Bedingung erfüllt sind, da wir φmax = 33.2° < φ = 40°, erhalten, während die zweite Bedingung φmax = 32.8° erfordert, siehe die grüne Variante in Abbildung (b).
Da die Projektionen beider Fließflächen in die Meridianebene vom Lode-Winkel abhängen, präsentieren wir diese Ergebnisse für den Fall der triaxialen Kompression. Details zur Vorhersage der Weichwerdung des Generalisierten Cam-Clay-Modells sind in der Modellbeschreibung zu finden, ebenso wie der Vergleich der Vorhersagen des Modifizierten Cam-Clay und Generalisierten Cam-Clay-Modells finden sie hier. Weitere Details finden sich im theoretischen Handbuch.
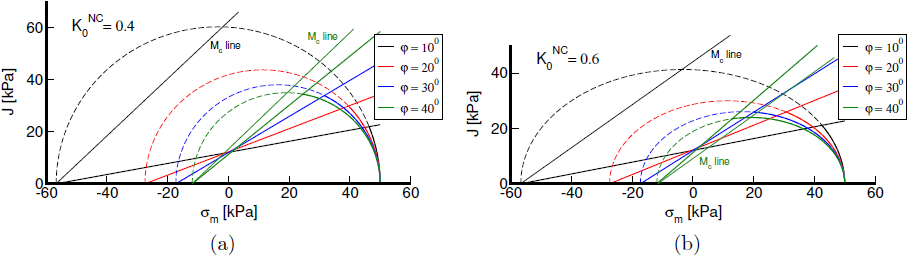Kompressions- und Scherspannungsflächen: φ und K0NC: a) K0NC =0.4, b) K0NC =0.6
Entwicklung des Vorkonsolidierungsdrucks pc sowie die Bedeutung der einzelnen Parameter, die die grundlegenden konstitutiven Beziehungen für die Kompressionskappe definieren, sind in der Beschreibung des Modifizierten Cam-Clay-Modells erläutert. Die plastische Potenzialfunktion, die die Entwicklung plastischer Dehnungen in dem von der Scherfließfläche kontrollierten Bereich beschreibt, ist mit der des Drucker-Prager-Modells identisch. Daher ist sie vom Lode-Winkel unabhängig. Auf der anderen Seite hängt sie vom Dilatanzwinkel ψ (Mψ = Mψ(ψ)). Im Allgemeinen nehmen wir an, dass φ ≠ ψ, was der nicht assoziierten Regel entspricht. Ähnlich wie beim Drucker-Prager-Modell kann die Menge der Dilatation (Entwicklung positiver volumetrischer plastischer Dehnungen während der plastischen Scherung) durch die Einführung des maximalen Porenverhältnisses emax begrenzt werden, für das der kritische Zustand ψ = 0 erwartet wird.
Parameter zur Definition des Soft Soil Materialmodells sind in der folgenden Tabelle zusammengefasst:
Symbol | Einheiten | Beschreibung | |
|
| Steigung der Schwellenlinie | |
|
| Steigung der normalen Konsolidierungslinie | |
|
| Maximales Porenverhältnis auf dem | |
|
| Poisson'sches Verhältnis | |
| [kPa] | Effektiver Kohäsionskoeffizient | |
|
| Effektiver Reibungswinkel | |
|
| Dilatanzwinkel | |
|
| Seitlicher Erddruckbeiwert im Ruhezustand für normal konsolidierten Boden | |
|
| Maximales Porenverhältnis zur Beendigung der Dilatation (bei limitierter Dilatation) | |
|
| Überkonsolidierungsverhältnis | |
| [kPa] | Überlastungsdruck | |
| [1/K] | Wärmeerweiterungskoeffizient (bei Berücksichtigung der Temperatureffekte) | |
|
| Kritischer Reibungswinkel des Zustands (nicht eingegeben) | |
| [kPa] | Preconsolidation pressure |
Diagramm
(not inputted)Ähnlich wie im Modifizierten Cam-Clay-Modell wird der Young-Modul der Elastizität nicht direkt eingegeben, sondern aus dem Volumenmodul Ks abgeleitet, das durch folgende Formel gegeben ist:
Offensichtlich hängt die Steifigkeitsentwicklung, wie im Fall des Modifizierten Cam-Clay-Modells, von der mittleren effektiven Spannung σm ab. Das Setzen der initialen Werte des Vorkonsolidierungsdrucks pcin ,des Volumenmoduls Ksin, und des initialen Porenverhältnisses 
wird im Detail in der Darstellung des Modifizierten Cam-Clay-Modells beschrieben.
Dies steht in engem Zusammenhang mit der Auswahl des initialen Lastschrittes, bei dem sehr niedrige Werte der Anfangsspannung erforderlich sind, um ausreichend klein zu sein. Um die Konvergenz zu beschleunigen, scheint es nützlich zu sein, die minimale Anzahl an Iterationen für einen einzelnen Lastschritt auszunutzen. Der Einfluss der Größe des initialen Lastschrittes auf die Entwicklung von Spannung und Dehnung wird hier im Detail beschrieben.
Im Gegensatz zu anderen Mohr-Coulomb-Modellen wird das initiale Porenverhältnis ein, das dem Zustand des Bodens zu Beginn des ersten Rechenschritts (geostatischer Druck) entspricht, nicht direkt eingegeben, sondern rechnerisch aus dem eingegebenen Wert des Porenverhältnisses e0 und dem aktuellen Spannungszustand bestimmt. Siehe auch die Beschreibung des Modifizierten Cam-Clay-Modells.
Das Modell ermöglicht die Anpassung des initialen Werts des Vorkonsolidierungsdrucks pc in Abhängigkeit vom erwarteten Grad der Vorkonsolidierung durch Verwendung der Parameter 
und 
. Weitere Details hierzu finden sich hier. Beachten Sie, dass diese Option nur verfügbar ist, wenn der initiale geostatische Druck mit Hilfe des K0 Verfahrens festgelegt wird.
Wenn ungesättigte Bedingungen für die Analyse erforderlich sind, kann die Analyse nur mit Typ (1): Analyse in effektiven Spannungen (cef, φe) fortgesetzt werden."
Das Weiche-Boden-Modell ermöglicht auch die Durchführung der Stabilitätsanalyse. Diese Option ist jedoch nur verfügbar, wenn die Stabilitätsanalyse während einer gegebenen Bauphase durchgeführt wird. In diesem Fall wird die Kompressionskappe deaktiviert. Daher kann nur die Scherspannungsoberfläche aktiv werden. Die Aufgabe wird durch schrittweises Reduzieren der maximalen Scherfestigkeitsparameter c, φ gelöst, wie es auch beim Drucker-Prager-Modell beschrieben ist.
Die Leistung des Modells im Rahmen einfacher Labortests wird hier untersucht, einschließlich des Vergleichs mit dem Modifizierten Cam-Clay-Modell und dem Einfluss der Größe des initialen Lastschrittes.
Die Implementierung des Weiche-Boden-Materialmodells in das GEO5 FEM-Programm wird im theoretischen Handbuch detailliert beschrieben.
Literatur:
[1] R.B.J. Brinkgreve, Geomaterial Models and Numerical Analysis of Softening, PhD thesis, Technische Universiteit Delft, 1994. Available at https://repository.tudelft.nl/record/uuid:6738de62-4dde-45b0-b3bd-3635504767c2.