Modifizeiertes Mohr-Coulomb-Modell (MCM)
Das modifizierte Mohr-Coulomb-Modell stellt eine Erweiterung des ursprünglichen Mohr-Coulomb-Modells dar. Die Versagensfläche wird ähnlich der Scherversagensfläche des Soft Soil-Modells oder der Grenzversagensfläche des Härtungsbodens dargestellt, in Form des Matsuo-Nakai-Versagenskriteriums. Dies wird in der folgenden Abbildung deutlich. Aus der Projektion der Versagensfläche in die deviatorischen Ebenen wird ersichtlich, dass mit sinkendem Innenreibungswinkel φ die Versagensfläche sich der Druck-Prager-Oberfläche nähert, während sie für höhere Werte von φ die Rankin-Oberfläche annähert. Darüber hinaus handelt es sich bei der Versagensfläche des modifizierten Mohr-Coulomb-Modells um eine glatte konvexe Kurve, die durch alle Eckpunkte des Mohr-Coulomb-Modells verläuft. Im Gegensatz zum Druck-Prager-Modell ist die Neigung der Projektion in die Meridianebene Mφθ jedoch nicht konstant, sondern hängt vom aktuellen Wert des Lode-Winkels ab (Mφθ = Mφθ(φ, θ)).
Im Gegensatz dazu ist die plastische Potentialfunktion, die die Entwicklung der plastischen Dehnungen steuert, identisch mit der des Druck-Prager-Modells. Sie ist daher unabhängig vom Lode-Winkel. Sie hängt jedoch vom Dilatationswinkel ψ ab (Mψ = Mψ(ψ)). Allgemein wird angenommen, dass φ ≠ ψ, was der nicht-assoziierten Fließregel entspricht.
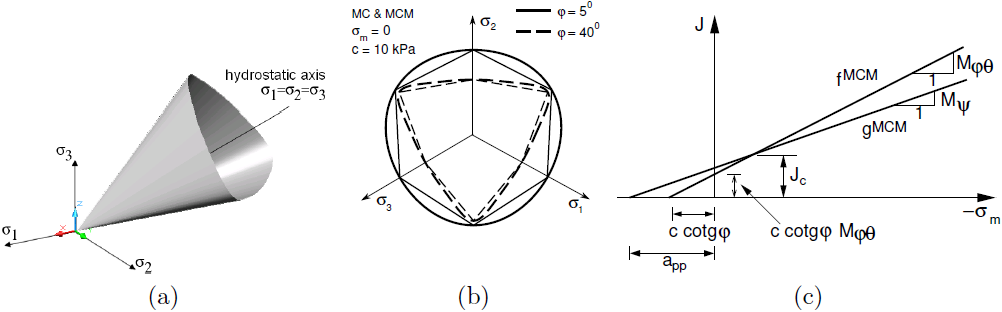 a) Versagensfläche im Raum der Hauptspannungen,, b) Projektion in die deviatorischen und c) Meridianebenen
a) Versagensfläche im Raum der Hauptspannungen,, b) Projektion in die deviatorischen und c) Meridianebenen
Im Unterschied zu anderen Modellen, unabhängig davon, ob elastisch-perfekt-plastisch oder elastisch-plastisch mit Härtung/Weichung, erlaubt das modifizierte Mohr-Coulomb-Modell die Entwicklung der Versagensfläche als Funktion der äquivalenten deviatorischen plastischen Dehnung Edpl. Genauer gesagt definieren wir die Funktionen c(Edpl) und φ(Edpl). Die angenommene, stückweise lineare Variation der Festigkeitsparameter ist in der folgenden Abbildung ersichtlich.
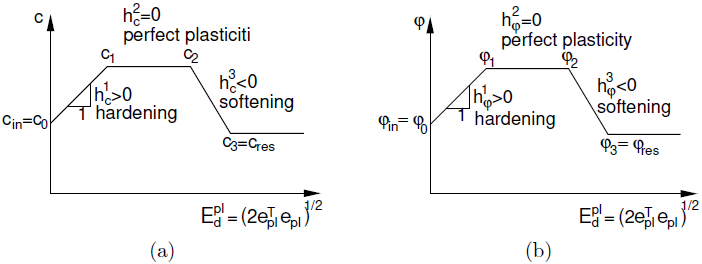 Entwicklung der Scherfestigkeitsparameter als Funktion der äquivalenten deviatorischen plastischen Dehnung Edpl: a) Kohäsion c b) Innenreibungswinkel φ
Entwicklung der Scherfestigkeitsparameter als Funktion der äquivalenten deviatorischen plastischen Dehnung Edpl: a) Kohäsion c b) Innenreibungswinkel φ
Wenn der Fokus auf einfachen Labortests (z. B. triaxiale Kompression) und auf elastisch-perfekt-plastische Reaktionen gelegt wird, liefert das Modell Vorhersagen, die denen des Druck-Prager- oder Mohr-Coulomb-Modells entsprechen.
Das gleiche gilt für die Anwendung bei dränierten oder undränierten Bedingungen. Weitere Informationen hierzu sind in der Präsentation des Druck-Prager-Modells verfügbar. Wenn die Analyse unter undränierten Bedingungen durchgeführt wird und Härtungs-/Weichungsmerkmale berücksichtigt werden, kann mit der Analyse des Typs (1) fortgefahren werden: Analyse in effektiven Spannungen (cef, φe)
Wenn der Effekt der Dilatation (Entwicklung positiver volumetrischer plastischer Dehnungen während plastischer Scherung) modelliert wird, erlaubt das modifizierte Mohr-Coulomb-Modell die Annahme entweder eines konstanten Dilatationswinkels ψ, ähnlich wie beim Druck-Prager-, Mohr-Coulomb- oder Hoek-Brown-Modell, oder die Beschreibung der Entwicklung von ψ unter Verwendung der Dilatationstheorie von Rowe, wie folgt:
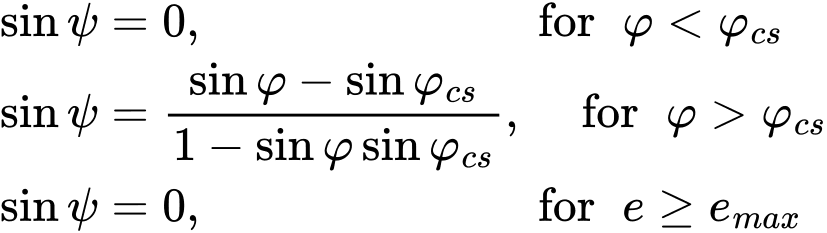
wobei φ den aktuellen Wert des Innenreibungswinkels und φcs den kritischen Scherwinkel darstellt. Es ist klar, dass die Entwicklung positiver volumetrischer Dehnungen mit Hilfe des maximalen Porenverhältnisses emax begrenzt werden kann, wie es beispielsweise beim Druck-Prager-Modell beschrieben wird.
Die folgenden Parameter werden für die Analyse unter undränierten Bedingungen verwendet, wobei für Typen 2 und 3 auf die Präsentation des Druck-Prager-Modells verwiesen wird.
Symbol | Einheiten | Beschreibung | |
| [MPa] | Elastizitätsmodul | |
| [MPa] | Modul für Entlastung/Wiederbelastung | |
|
| Poisson’sche Zahl | |
| [kPa] | Effektiver Kohäsionskoeffizient | |
| [°] | Effektiver Innenreibungswinkel | |
| [°] | Dilatationswinkel | |
| [kN/m3] | Schüttgewicht | |
|
| Initiales Porenverhältnis, das dem Zustand am Ende des ersten Bauphase entspricht | |
|
| Maximales Porenverhältnis, um die Dilatation zu beenden (bei Begrenzung der Dilatation) | |
| [°] | Kritischer Scherwinkel (bei Bestimmung von | |
| [1/K] | Koeffizient der thermischen Ausdehnung (bei Berücksichtigung von Temperatureffekten) | |
| - | Graph, der die Entwicklung von c als Funktion von |
Der Modifizierte Mohr-Coulomb-Modell ermöglicht die Durchführung von Stabilitätsanalysen. Sowohl die Standard-Böschungsstabilitätsanalyse als auch die Stabilitätsanalyse innerhalb einer gegebenen Bauphase können durchgeführt werden. Die Aufgabe wird durch die schrittweise Reduzierung der maximalen Scherfestigkeitsparameter c, φ gelöst, wie es im Druck-Prager-Modell beschrieben ist. Während des Reduktionsprozesses wird das Härtungs-/Weichungsmerkmal deaktiviert.Es wird erwartet, dass das Modell durch die Einführung der Kap-Versagensfläche weiter verbessert wird, ähnlich wie beim Soft Soil Modell.