Hardening soil
Das Hardening Soil Modell, eingeführt von Schanz et al. [1], eignet sich zur Modellierung von Böden mit großem Gruppenverhalten. Das Modell kombiniert zwei Verfestigungsmechanismen. Der Schermechanismus steuert die Entwicklung plastischer Dehnungen, die durch deviatorische Spannungsanteile verursacht werden, während der Kompressionsmechanismus aktiv wird, wenn die Last in Kompression erfolgt, z. B. im Oedometer oder bei isotroper Kompression. Der Scher-Verfestigungsmechanismus äußert sich in einer graduellen Evolution der Scherfließfläche fsHS in Abhängigkeit vom aktuellen Wert der äquivalenten deviatorischen plastischen Dehnung κs(oder γps).
Dieser Verfestigungsprozess (Expansion der Fließfläche) wird begleitet von der Entwicklung des mobilisierten Winkels der internen Reibung φm und endet mit dem Erreichen der Grenz-Scherfließfläche fsMN. Im GEO5 FEM-Programm wird diese Fließfunktion in Form des Matsuoka-Nakai-Versagens-Kriteriums dargestellt, das die Funktion der Spitzenwerte der Scherfestigkeitsparameter, der Kohäsion c, und des Winkels der internen Reibung φ darstellt. Die Projektion der Fließfläche in den deviatorischen Raum ist daher eine glatte konvexe Kurve, die durch alle Eckpunkte des Mohr-Coulomb Modells verläuft. Die Folge der Kompressionsverfestigung ist eine Entwicklung der Kapazitätsfließfläche fcHS in Abhängigkeit von der Entwicklung des Prekonsolidierungsdrucks pc. Eine ähnliche Formulierung, die in Bezug auf invariante Spannungsmaße entwickelt wurde, wurde ebenfalls in [2] vorgestellt.
Eine grafische Darstellung beider Fließflächen ist in der folgenden Abbildung ersichtlich. Eine allmähliche Entwicklung der Scherversagensfläche, die durch die Projektion der Fließfläche in die Meridianebene dargestellt wird, wird zur Veranschaulichung gezeigt. In ähnlicher Weise wird das Soft-Soil-Modell definiert, das jedoch nur die Grenzscherversagensfläche implementiert. Das Härten ist daher auf die kompressive Kappe begrenzt.
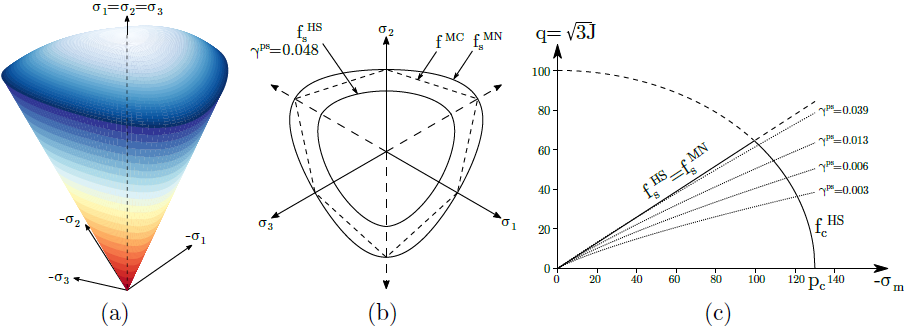 a) Fließfläche im Hauptspannungsraum, b) Projektion in den deviatorischen Raum und c) Projektion in die Meridianebene
a) Fließfläche im Hauptspannungsraum, b) Projektion in den deviatorischen Raum und c) Projektion in die Meridianebene
Formulierung der Scherversagensfläche basiert auf der Annahme, dass die Beziehung zwischen der deviatorischen Spannung q und der vertikalen Dehnung ε3 während des entlasteten triaxialen Tests durch eine hyperbolische Funktion beschrieben werden kann. Das entsprechende Spannungs-Dehnungs-Diagramm ist in der folgenden Abbildung gezeigt, wobei qa den asymptotischen Wert von q darstellt und qfMC den Wert von q beim Erreichen der Grenzfläche, in welchem Fall gilt qf = Rfqa, wobei Rf der Reduktionskoeffizient ist. Weitere Details sind im theoretischen Handbuch zu finden.
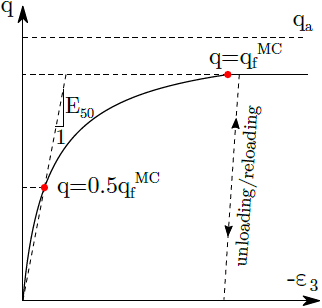 Hyperbolisches Spannungs-Dehnungs-Gesetz
Hyperbolisches Spannungs-Dehnungs-Gesetz
Die Parameter, die das Materialmodell für den Härteboden definieren, sind in der folgenden Tabelle zusammengefasst.
Symbol | Einheiten | Beschreibung | |
| [MPa] | Sekantenmodul der Elastizität | |
| [MPa] | Modul des Ent- und Beladens | |
| [-] | Poisson'sches Verhältnis | |
| [kPa] | Referenzmittelspannung | |
| [-] | Exponent der Steifigkeitsgesetzmäßigkeit | |
| [kPa] | Grenzwert der Mittelspannung, um eine nicht-null Steifigkeit zu gewährleisten | |
| [kN/m3] | Schüttgewicht | |
| [-] | Initiales Porenverhältnis zum Zustand am Ende des ersten Rechenschritts | |
| [-] | Versagensverhältnis | |
| [kPa] | Spitzenwirksame Kohäsion | |
| [°] | Spitzenwirksamer Reibungswinkel | |
| [°] | Dilatanzwinkel | |
| Schüttgewicht | ||
| [-] | Seitlicher Erddruckbeiwert im Ruhezustand für normal konsolidierten Boden | |
| [MPa] | Tangentialer edometrischer Modul | |
| [kPa] | Referenzvertikale Spannung zur Bestimmung vonA | |
| [-] | Maximales Porenverhältnis zur Beendigung der Dilatation (bei limitierter Dilatation) | |
| [-] | Überkonsolidierungsverhältnis | |
| [kPa] | Überlastungsdruck | |
| [1/K] | Wärmeerweiterungskoeffizient (bei Berücksichtigung der Temperatureffekte) | |
| [-] | Parameter zur Definition der Form der Kompressionskappe | |
| [Pa] | Härtemodul (nicht eingegeben) | |
| [kPa] | Vorkonsolidierungsdruck | |
| [°] | Kritischer Reibungswinkel (nicht eingegeben) | |
| [°] | Mobilisierter Reibungswinkel des inneren Reibens (nicht eingegeben) | |
| [°] | Mobilisierter Dilatanzwinkel (nicht eingegeben) |
Die Sekantenmodul der Elastizität Eip,ref kann mit Hilfe des Moduls der Elastizität E50p,ref wie folgt approximiert werden:
![]()
Dabei stellt (p,ref) einen Referenzwert des Moduls für eine bestimmte Mittelspannung σmref dar. Im Allgemeinen nimmt das Modell eine Entwicklung des Elastizitätsmoduls als Funktion der aktuellen Mittelspannung in der Form an:
![]()
Beachten Sie, dass diese Formulierung sich von der in den Publikationen [1] und [2] verwendeten unterscheidet, in denen die Entwicklung der Steifigkeit von der minimalen Hauptspannung abhängt σ1. Dies sollte berücksichtigt werden, wenn Parameter übernommen werden, die für eine andere Ingenieurssoftware, wie das GEO5 FEM-Programm, kalibriert wurden. Eine mögliche Option besteht darin, einen modifizierten Parametersatz zu verwenden, der zu einer vernünftigen Übereinstimmung der Simulationen führt, die von einzelnen Softwarepaketen bereitgestellt werden. Zu diesem Zweck erscheint eine einfache lineare Regression als ausreichend, um die Parameter Eurp,ref und mpanzupassen. Ein anschauliches Beispiel für diesen speziellen Ansatz wird in der folgenden Abbildung dargestellt.
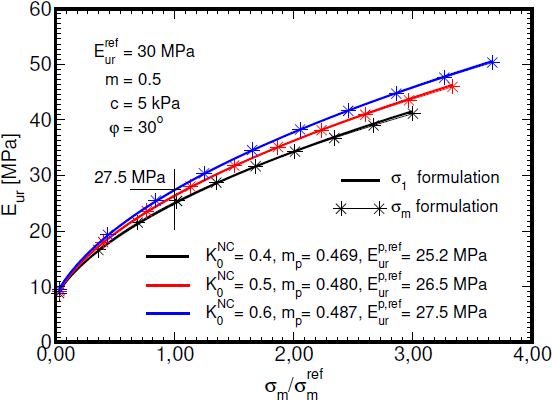 Bestimmung der Abhängigkeit des Moduls von Ent-/Beladung Eur von der Mittelspannung σm unter Verwendung der linearen Regression
Bestimmung der Abhängigkeit des Moduls von Ent-/Beladung Eur von der Mittelspannung σm unter Verwendung der linearen Regression
Die modifizierten Parameter E50p,ref(Eip,ref) und Rf können anschließend innerhalb eines Optimierungsschritts ermittelt werden, indem numerische Simulationen eines triaxialen Kompressionstests verglichen werden, wobei bereits bestimmte Parameter Eurp,ref und mpausgenutzt werden.
Weitere Details sind im theoretischen Handbuch zu finden. Es wird jedoch dringend empfohlen, die spezifischen Modellparameter, die mit einer bestimmten Implementierung verbunden sind, aus den bereitgestellten Labormessungen zu kalibrieren, beispielsweise mit der Kalibrierungssoftware ExCalibre.
Die Kompressionskappe fcHS wird durch den Parameter M charakterisiert, der ihre Form bestimmt, und durch das Härtemodul H das die Erhöhung des Vorkonsolidierungsdrucks Δpc in Bezug auf die Erhöhung der volumetrischen plastischen Dehnung Δεvpl angibt. Das Härtemodul The hardening modulus H wird durch folgende Gleichung gegeben:
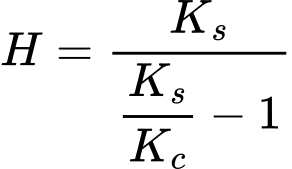
wo Kc, Ks die Volumenmoduli bei primärer Belastung und Entlastung sind. Weitere Details sind im theoretischen Handbuch verfügbar. Die Parameter können entweder direkt eingegeben oder automatisch basierend auf den Werten des seitlichen Erddruckbeiwerts K0NC und des edometrischen Moduls Eoedref.bestimmt werden. Dies wird durch numerische Optimierung eines edometrischen Labortests erreicht. Das Ziel ist es, die Modellparameter M, H zu bestimmen, sodass das numerisch vorhergesagte edometrische Modul mit dem für einen gegebenen Wert von K0NC angegebenen Modul übereinstimmt, wie aus der folgenden Abbildung ersichtlich ist. Die Mittelspannung σm* und der äquivalente deviatorische Stress J* werden durch folgende Formeln gegeben:

Weitere Details sind im theoretischen Handbuch zu finden.
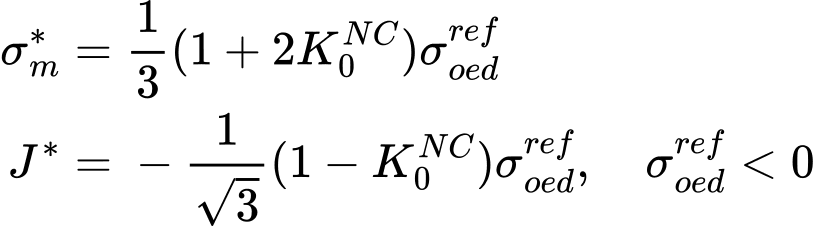 a) Graphische Darstellung des Referenz-Edometrischen Moduls Eoedref zu einem angegebenen Punkt des σoedref, b) Aktueller Stress am Ende des Optimierungsschritts, der mit σoedref
a) Graphische Darstellung des Referenz-Edometrischen Moduls Eoedref zu einem angegebenen Punkt des σoedref, b) Aktueller Stress am Ende des Optimierungsschritts, der mit σoedref
verbunden ist.
Das Härtebodenmodell dient der Modellierung der Boden-Dilatation (Entwicklung positiver volumetrischer plastischer Dehnungen während der plastischen Scherung) durch die Einführung des Dilatanzwinkels ψ getrieben. Die Entwicklung der plastischen Dehnungen wird durch das plastische Potential gsHS. Die Definition des plastischen Potentials ist im Wesentlichen identisch mit dem des Drucker-Prager-Modells. Der einzige Unterschied liegt in der Definition der Steigung des plastischen Potentials Mψ das nun vom aktuellen Wert des mobilisierten Reibungswinkels ψmabhängt. Die entsprechende Evolutionsgleichung folgt ähnlich dem Modifizierten Mohr-Coulomb-Modell und der Rowe-Dilatationstheorie:
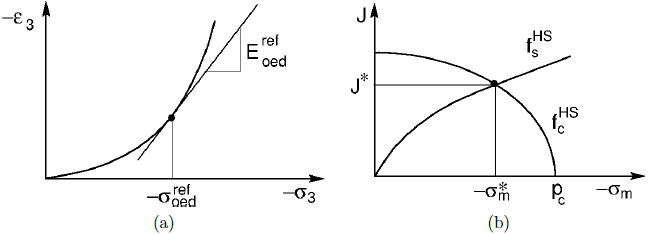
wobei φ, φm, φcs, ψ die Spitzenwerte des inneren Reibungswinkels, des mobilisierten inneren Reibungswinkels, des kritischen Reibungswinkels und des Dilatanzwinkels sind. Eine grafische Darstellung der Entwicklung von ψm ist aus der folgenden Abbildung ersichtlich. Sie zeigt auch eine potenzielle Dilatanz-Begrenzung, die durch die Einführung des maximalen Porenverhältnisses emaxerreicht wird, bei dem der kritische Zustand ψm = 0 erwartet wird
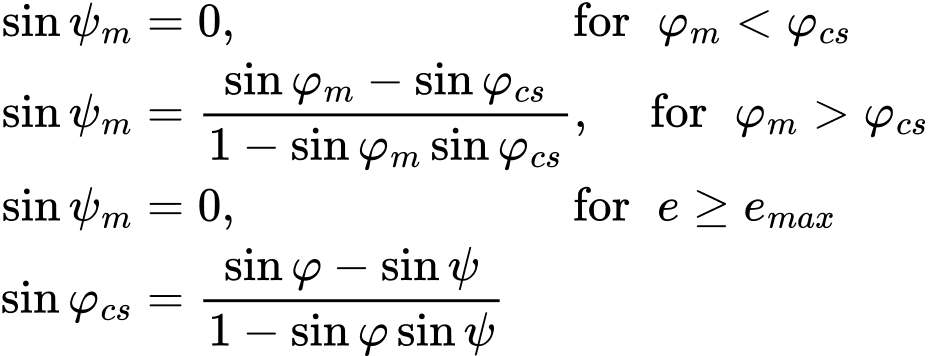 Rowe Dilatationstheorie:: a) Grafische Darstellung der Entwicklung des mobilisierten Dilatanzwinkels ψm, b) Dilatanz-Begrenzung
Rowe Dilatationstheorie:: a) Grafische Darstellung der Entwicklung des mobilisierten Dilatanzwinkels ψm, b) Dilatanz-Begrenzung
Beachten Sie, dass die Steifigkeitsentwicklung vom aktuellen Wert der mittleren effektiven Spannung σm abhängt. Dies ist eng mit der Auswahl des initialen Lastschrittes verbunden, der sehr niedrige Werte der Anfangsspannung erfordert, um sicherzustellen, dass die Lasten ausreichend klein sind. Um die Konvergenz zu beschleunigen, scheint es nützlich zu sein, die minimale Anzahl an Iterationen für einen einzelnen Lastschritt auszunutzen. Der Einfluss der Größe des initialen Lastschrittes auf die Entwicklung von Spannung und Dehnung wird im Detail hier beschrieben.
Ein wichtiger Punkt im Hinblick auf eine erfolgreiche Analyse ist die Festlegung der initialen Werte des Vorkonsolidierungsdrucks pcin und der äquivalenten plastischen deviatorischen Dehnung κsin, die in Abhängigkeit vom aktuellen Spannungszustand zu dem Zeitpunkt gesetzt werden, an dem das Härtebodenmodell eingeführt wird. Beide Parameter werden so eingestellt, dass der aktuelle Spannungszustand den Anforderungen des Härtebodenmodells entspricht. Details sind hier beschrieben. Es ist auch möglich, das Modifizierte Cam-Clay-Modell zu konsultieren.
Das Modell erlaubt auch die Anpassung des initialen Werts des Vorkonsolidierungsdrucks in Abhängigkeit vom zu erwartenden Grad der Vorkonsolidierung durch Verwendung der Parameter ![]() und
und ![]() . Details hierzu finden Sie hier. Beachten Sie, dass diese Option nur verfügbar ist, wenn der initiale geostatische Druck mit Hilfe des K0 Verfahrens festgelegt wird.
. Details hierzu finden Sie hier. Beachten Sie, dass diese Option nur verfügbar ist, wenn der initiale geostatische Druck mit Hilfe des K0 Verfahrens festgelegt wird.
Wenn ungesättigte Bedingungen für die Analyse erforderlich sind, kann die Analyse nur mit effektiven Spannungen (cef, φe) fortgesetzt werden.
Das Härtebodenmodell ermöglicht auch die Durchführung der Stabilitätsanalyse. Diese Option ist jedoch nur verfügbar, wenn die Stabilitätsanalyse während einer gegebenen Bauphase durchgeführt wird. In diesem Fall wird die Kompressionskappe deaktiviert, ebenso wie die Entwicklung des mobilisierten Reibungswinkels. Daher kann nur die Grenzgrenze fsMN aktiviert werden. Die Aufgabe wird durch schrittweises Reduzieren der maximalen Scherfestigkeitsparameter c, φ gelöst, wie es auch beim Drucker-Prager-Modell beschrieben ist.
Die Leistung des Modells im Rahmen einfacher Labortests wird hier untersucht, einschließlich des Einflusses der Größe des initialen Lastschrittes.
Es wird empfohlen, die Parameter des Härtebodenmodells nur dann zu verwenden, wenn es klare experimentelle Beweise für unterschiedliche Werte gibt, da sie innerhalb der empfohlenen Bereiche in der folgenden Tabelle liegen sollten.
Symbol | Einheit | Empfohlener Wert | |
| [MPa] | (2, 70) | |
| [MPa] |
| |
| [kPa] | 100.0 | |
| [-] | (0.3, 0.9) | |
| [kPa] | 10.0 | |
| [-] | 0.9 | |
| [°] | (16.0, 42.0) | |
| [kPa] | (0.0, 50.0) | |
| [°] |
| |
| [-] | (0.5, 2.5) | |
| [-] | 0,2 | |
| [-] |
| |
| [-] |
| |
| [kPa] | 100.0 | |
| [MPa] |
|
Die Implementierung des Härtebodenmaterialmodells in das GEO5 FEM-Programm wird im theoretischen Handbuch detailliert beschrieben.
Literatur:
[1] T. Schanz, P.A. Vermeer, P.G. Bonnier, The hardening soil model: Formulation and verification, Beyond 2000 in Computational Geotechnics, Balkema, Rotterdam. 1999
[2] T. Benz, Small-Strain Stiffness of Soils and its Numerical Consequences, PhD thesis, University of Stuttgart, 2007