Как пользоваться справкой
Справка программ GEO5 отображается в стандартном диалоговом окне. Диалоговое окно справки открываем в меню программы (пункты «Справка», «Содержание»), или функциональной кнопкой «F1» в любом месте программы.
В некоторых диалоговых окнах (напр., «Добавление новых грунтов») можно соответствующий раздел справки открыть, нажав кнопку справки «![]() » .
» .
В диалоговом окне находятся:
- Панель с основными кнопками управления. Кнопка «Печать» откроет системное окно для печати. Кнопки «Назад / Вперёд» позволяют перелистывать отображенные страницы. Кнопки «Предыдущий / Следующий» позволяют перемещение между пунктами в «дереве» вверх или вниз.
- Поле ввода «Поиск».
- Древообразный список пунктов справки – отдельные папки в дереве открываются / закрываются щелчком на символ перед названием «
 »/«
»/« ».
». - Окно для собственно изображения справки – заголовок окна содержит имя текущей изображённой страницы.
Текст справки содержит контекстные ссылки на остальные пункты. Текст контекстных ссылок выделен зелёным цветом.
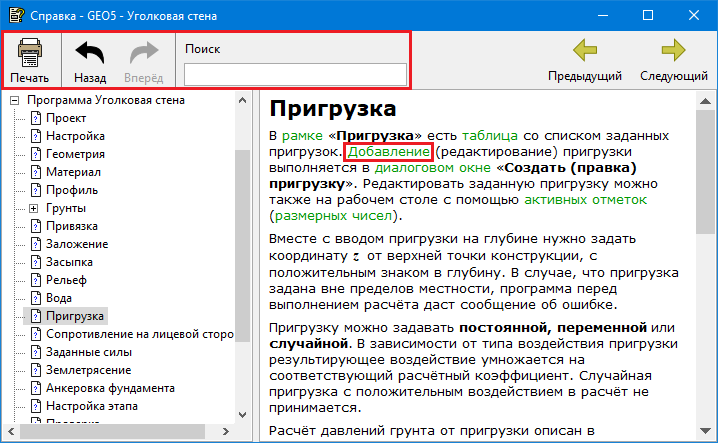 Диалоговое окно «Справка - GEO5»
Диалоговое окно «Справка - GEO5»